Super Soaker Central

From previous articles, I have defined output as the rate of change of the water already shot out of a soaker. I have also defined it as the negative rate of change of amount of water in the chamber. I now introduce a vectorized method of calculate output.

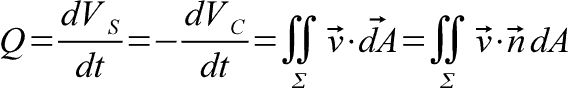
Output is the surface integral of a velocity field over a parameterized surface. This method allow calculation of a flow over an area with a varying velocity profile. The dot product shows that only velocity in the direction of the surface counts towards the flow rate. The n-hat is a unit vector in the normal of the parameterized surface.

Deriving the "simple output" formula

The equation given above may seem far too advanced and general; but that is its advantage: how general and simple it is. A special case of this is everyone's favorite "simple output" formula for an area with an average velocity.

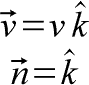
Let's define a velocity field as uniform with a velocity v in the z-direction (coming out of the xy-plane). Let's also define our surface as the xy-plane--the z-direction is normal to this.

Applying this to the formula yields a simple answer. k-hat dot k-hat is 1, so it simplifies to the double integral of surface sigma of vdA.

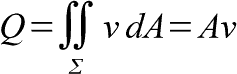
If we define the area of surface sigma as A, the equation simplies to to the simple and easy to remember Q=Av.